My latest supplement on the DM’s Guild, The Hand You’re Dealt, provides instructions on how to generate a character’s ability scores by way of a quick solitaire card game. I hope it helps you create memorable characters, and that you find the method fun in itself!

I think the mathematics that drove some of my decisions are pretty interesting, but in an ancillary sort of way. So rather than stuff it in the product, I’m including it here for anyone interested enough to take a gander.

I spilled enough pixels in the PDF about what makes playing cards an interesting alternative to dice, and how this method will produce an ability score curve with unique contours. But I wanted to ensure that this method would produce characters that could fit in with those made via more traditional means.

“4d6 drop the lowest” is probably the most common method, so let’s start there. AnyDice analyzed the probabilities pretty thoroughly and found that, on average, that method produces the following spread: 16, 14, 13, 12, 10, 9. This gives us a good idea of the minimum and maximum scores a player might expect, but we already know we’re going to blow the bloody doors off both of those numbers.

More useful to us is the knowledge that this average spreads 74 points over six abilities. That’ll provide a better metric to compare our cards against. We should also account for the fact that our method allows the player to allocate points in such a way that they can result in extremely high and extremely low scores, more frequently than if left to chance. 

I actually prefer to roll 3d6 if I’m using dice to roll ability scores. A similar analysis of that approach shows that we’re likely to wind up with a collection of scores like this: 14, 12, 11, 10, 9, 7. This pool is a little shallower, giving the player 63 points.

Looking at diceless methods, the Standard Array comes in just a whit behind 4d6: 15, 14, 13, 12, 10, 8, totaling 72 points. Precisely 64 different ability score spreads are possible using Point Buy; because high scores cost more than lower ones, they can give the player anywhere from 69 to 75 points, averaging 72.32, with no scores below 8. (Yawn!)

Both examples in The Hand You’re Dealt come in pretty low compared to those metrics. Round 1 totals 68 points, and Round 2 gives only a paltry 58 points! However, I think those points are distributed in a way that can result in an entirely playable character. I also would like to err on the side of providing slightly fewer points than average, because by allowing the player some amount of choice in the outcome, they’re more likely to achieve at least one outstanding score.

Now seems as good a time as any to talk about the range of scores that are possible with this method. If the unluckiest newbie dealt themselves the worst possible cards, it would result in a pool of 50 points; conversely, the most fortunate would have 94 points to play with. (!!!)

But those are both cosmically unlikely circumstances. (If someone wants to run those numbers, I’ll update this post.) Technically, rolling 3d6, you could end up with a range of 18 – 108 stat points, but that’s probably even more unlikely. Once again, we should focus on the most likely scenarios.

The example plays presented in the supplement are real hands that I dealt myself, selected for their demonstration of certain features of play. But they’re also uncommonly low-scoring, compared to the average.

I wrote a quick and (very) dirty PHP script that could simulate and keep track of ten thousand deals, in order to provide some reliable averages. Here’s how that went.

Originally, I was only going to include two Sevens in the deck, so the possible scores would hew closer to what dice could actually provide. That generated scores lower than I would have liked, though, producing a mean pool of 67.43 points. Including the full set of Sevens in the deck increased the average pool of points to 70.77. That’s straight between the goalposts provided by 3d6 and 4d6-drop-the-lowest, and it’s also in line with the Standard Array and Point Buy methods.

We could actually get even closer to the 72.32 mean pool offered by Point Buy’s 64 different possibilities by including two Eights in the deck. That would bring the mean score up to 73.8565, practically in lock-step with those other methods. But there are other factors to consider. First of all, when using the deck with four Sevens, 14.15% out of my 10,000 deals resulted in at least one bust. Including two Eights cranks that up to 37.56% of deals. Since busts are (almost) entirely up to dumb luck rather than any kind of skill, having more than a third of rounds result in a bust seems a little high to me.

Additionally, certain scores will be more likely to appear than others, for the same reason that rolling 3d6 creates a nice bell curve — there are more ways to get a score of 11 than there are to get a score of 3 or 18. Our cards also make a bell curve. Here’s the distribution offered by the deck containing four Sevens and no Eights:

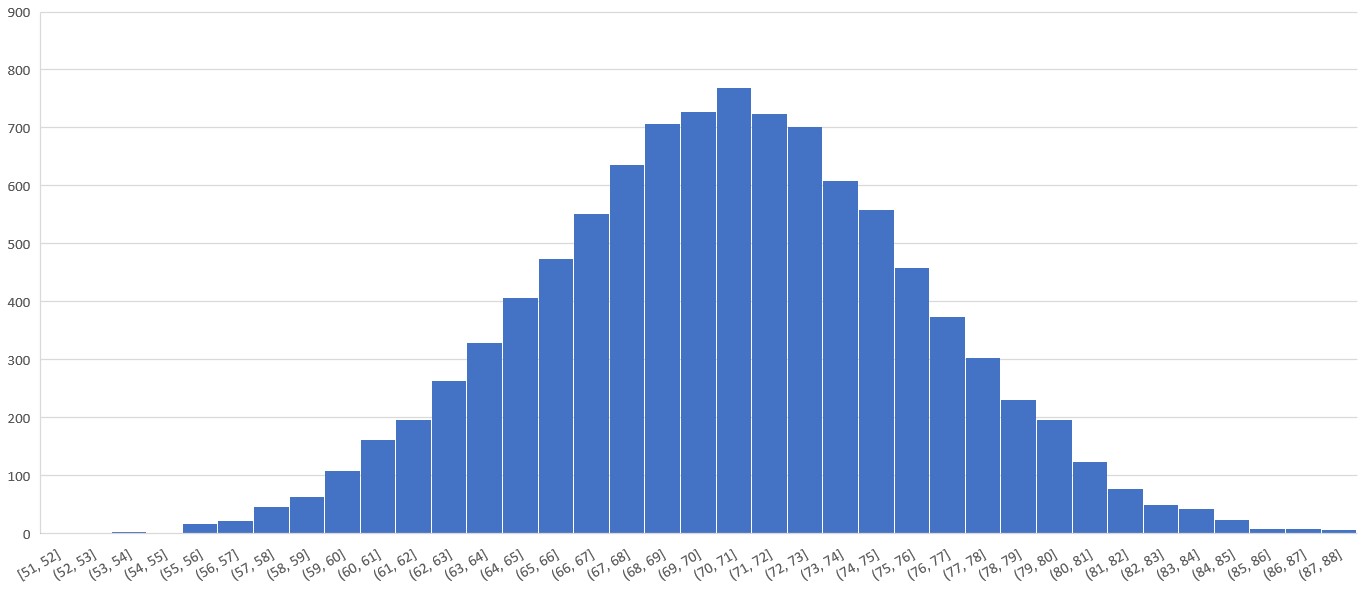
Players can reasonably expect to be working with 67 – 77 points to build their characters. That seems entirely reasonable to me, and I wouldn’t want to go much higher. Capping the deck at Sevens seems like the right choice. You may disagree, in which case I say include those Eights!

Including two more cards in either direction results in a pretty reliable three-point shift in the mean score. I originally included only two Sevens in the deck, but with an average of only 67.43 points per round, that was too low. Plus, fewer than 5% of rounds would see a bust with only two Sevens — that seemed too low. With four Eights, scores averaged 76.5 and 60% of rounds saw a bust; with two nines, average scores were 79.12 and a bust was practically guaranteed, showing up in 97.34% of all rounds played.

Being reasonably confident with that decision, I used that 28-card deck when testing my optional rules. And interestingly enough, while those optional rules increase the complexity for the player, I was pleasantly surprised to see that they didn’t mess up the averages too much.

For instance, when allowing three-of-a-kind to be dealt a fourth card, average points were essentially unaffected with a mean value of 70.94. Busts didn’t even increase by a full percentage point, even though, for simplicity’s sake, I was dealing a fourth card to *any* set of three, including three Sixes. (Three Sevens would already be counted as a bust and would be discarded before seeing a fourth card.) Additionally, 4.63% of all rounds saw a three-of-a-kind. I like those odds. That means if you have a group of five people generating characters at a session zero, maybe one of them will get a chance to deal a fourth card.

Finally, allowing for three Aces to bust also had little effect on the averages. Only around 1% of rounds saw that happen, and the average point total was essentially unchanged at 70.91.

I approximated the effect of adding two Jokers to the deck by instead adding two Fives and seeing how that changed the scores. In short, it didn’t noticeably move the needle in any direction. It’s not a perfect way to test it, but being a one-person operation with a limited and outdated knowledge of PHP, that was the best I could do.

I’m confident enough that this work holds up to scrutiny. I hope you agree, and either way, I’d love to hear what you think about this method of character creation.

The Hand You’re Dealt is available as a Pay-What-You-Want download on the DM’s Guild.